What is Reliability?
Reliability is the probability that an item will perform a required function under stated conditions for a stated period of time. The probability of survival, R(t), plus the probability of failure, F(t), is always unity.
F(t) + R(t) = 1 or F(t) = 1 - R(t)
The required function includes both a definition of satisfactory and unsatisfactory operation (failure). The stated conditions are the total physical environment, including mechanical, thermal, and electrical conditions. The stated period of time is the time during which satisfactory operation is desired.
What is Availability?
The probability that a system is in its intended functional condition and therefore capable of being used in a stated environment. Availability deals with the duration of up-time for operations and is a measure of how often the system is alive and well. It is often expressed as (up-time)/(up-time + downtime) with many different variants. Up-time and downtime refer to dichotomized conditions. Up-time refers to a capability to perform the task and downtime refers to not being able to perform the task.
What is Failure?
Failure is any event that impacts a system in a way that adversely affects the system criteria. For example, the criteria could include output in a sold-out condition, or maintenance cost or capital resources in a constrained budget cycle, environmental excursions or safety, etc. A failure definition should contain specific criteria and not be ambiguous. Failure definition can change on a given system over time.
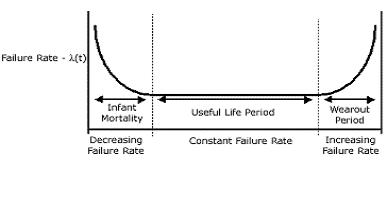
Field failures do not generally occur at a uniform rate, but follow a distribution in time commonly described as a "bathtub curve." The life of a device can be divided into three regions: Infant Mortality Period, where the failure rate progressively improves; Useful Life Period, where the failure rate remains constant; and Wearout Period, where failure rates begin to increase.
Within a population of units is a small sub-group of units with latent defects that will fail when exposed to a stress that would otherwise be benign to a good unit. With the failure of the weak units, the remaining population is more reliable, and the failure rate is known to decrease.
Units that pass the Infant Mortality Period have a high probability of surviving the conditions provided by the system and its environment. Failures that occur during the Useful Life Period are residual defects surviving Infant Mortality, unpredictable system or environmental conditions, or premature wearout.
Wearout failures are generally associated with such failure mechanisms as metal migration, hot electron effects, wirebond intermetallics, or thermal fatigue. Typically, the wearout of a semiconductor occurs after many years or even decades, and outlives the lifespan of the system in which the component is used.
What is Maintainability?
A measure of the ease and rapidity with which a system can be restored to operational status following a failure. Maintainability deals with duration of maintenance outages or how long it takes to achieve (ease and speed) the maintenance actions compared to a datum. The datum includes maintenance (all actions necessary for retaining an item in, or restoring an item to, a specified, good condition) is performed by personnel having specified skill levels, using prescribed procedures and resources, at each prescribed level of maintenance. Maintainability characteristics are usually determined by equipment design which set maintenance procedures and determine the length of repair times.
What is Failure Mode?
A particular way in which failures occur, independent of the reason for failure.
What is Early Life Period?
The early life period of device operation is characterized by a rapidly declining failure rate. It occurs between 0 and 10,000 hours (~1 year) of device operation. Ambient operating temperature is specified to be 55?C. The failure rate during the early life period can be modeled by the Weibull Distribution:
l(t) = lot-a
where 0 < a < 1. l(t) is usually expressed in percent failures per 1,000 hours.
What is Useful Life Period?
Beyond the infant mortality period, in the useful life period, the failure rate is assumed to be determined by the exponential distribution. The failure rate here is at its lowest and relatively constant during this period. It begins after 10,000 hours (~1 year) of device operation. Reliability during this period must be specified as a single, essentially constant failure rate. An operating temperature of 55?C, an activation energy of 0.62eV and normal operating voltage are used for lifetime and reliability calculations.
What is Failure Rate?
The number of failures of an item per unit measurement of life. Failure rate is considered constant over the useful life period.
What is Failure Modes and Effects Analysis (FMEA)?
A modified methodology to identify the modes of failure events and assigning values to them based on unit cost and frequency, then prioritizing the result in order to focus the organization on the significant few failures.
What is Failure Modes, Effects and Criticality Analysis (FMECA)?
This the the detailed version of FMEA. Instead of examining the system as larger units, you assign criticality values of each failure for the smallest units in the system that is observed.
What is Mean Time Between Failures (MTBF)?
Total operating time divided by the number of failures. MTBF is the inverse of failure rate.
What is Mean Time To Restore (MTTR)?
Total elapsed time from initial failure to the reinitiating of system status. Mean Time To Restore includes Mean Time To Repair (MTBF + MTTR = 1.)
What is Root Cause Failure Analysis (RCFA)?
A technique for uncovering the cause of a failure by deductive reasoning down to the physical and human root(s), and then using inductive reasoning to uncover the much broader latent or organizational root(s).